Оптимизация зоны технического обслуживания автомобилей автомобильного предприятия на основе системы массового обслуживания

,

- среднее количество требований (автомобилей), находящихся в очереди:

,

- среднее время нахождения автомобилей в очереди, час:

,

- количество обслуживаний за время моделирования:

,

где ТМОД – время моделирования зоны ТО-1, час.

Принимаем время моделирования равным 1 месяц для удобства расчёта суммарных затрат. Тогда время моделирования в часах определяется:

,

где длительность смены ТСМ=8 часов, количество смен С=1, количество дней работы зоны ТО-1 в месяц ДРАБ.МЕС.=252 дня/12=21 день.

ч.

Результаты расчёта сведём в таблицу 2.3.

Таблица 2.3 – Расчёт показателей эффективности СМО при моделировании зоны ТО-1

Расчёты представим также в виде графиков (см. рис. 1-7)

Рисунок 2.1 – Зависимость приведённой плотности потока требований ρ от количества постов ТО-1

Рисунок 2.2 – Зависимость вероятности образования очереди П от количества постов ТО-1

Рисунок 2.3 – Зависимость вероятности отказа в обслуживании РОТК от количества постов ТО-1

Рисунок 2.4 – Зависимость число занятых обслуживающих аппаратов (число занятых постов ТО-1) nЗАН от количества постов ТО-1

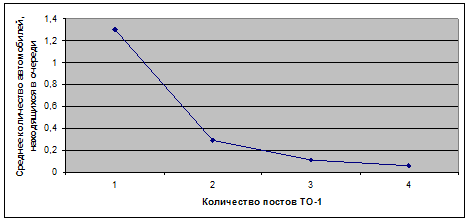
Рисунок 2.5 – Зависимость среднее количество требований (автомобилей), находящихся в очереди, r от количества постов ТО-1

Рисунок 2.6 – Зависимость среднее время нахождения автомобилей в очереди tОЖ, час, от количества постов ТО-1